Title: Adding and Subtracting Fractions with Unlike Denominators Worksheets PDF
Master adding and subtracting fractions with unlike denominators using our PDF worksheets․ These resources provide structured practice for common denominators, equivalent fractions, and real-world applications․
Importance of Common Denominators in Fraction Operations
Common denominators are essential for simplifying fraction operations, enabling straightforward addition and subtraction․ They allow fractions to be combined easily, making calculations more efficient and accurate․
2․1․ Steps to Add/Subtract Unlike Fractions
To add or subtract fractions with unlike denominators, follow these steps:
Identify the denominators of the fractions involved․
Find the Least Common Denominator (LCD) of these denominators․
Rewrite each fraction as an equivalent fraction with the LCD as the denominator․
Once the fractions have the same denominator, add or subtract the numerators while keeping the denominator the same․
Simplify the resulting fraction, if possible․
These steps ensure that fractions with different denominators can be combined accurately and efficiently․
2․2․ Finding the Least Common Denominator (LCD)
Finding the Least Common Denominator (LCD) is crucial for adding or subtracting fractions with unlike denominators․ The LCD is the smallest number that both denominators can divide into evenly․ To find it, list the multiples of each denominator and identify the smallest common multiple․ Alternatively, break down the denominators into their prime factors and multiply the highest powers of all prime factors involved․ This method ensures accuracy and efficiency․ For example, to find the LCD of 4 and 6, list the multiples: 4, 8, 12, 16 and 6, 12, 18․ The smallest common multiple is 12․ Using prime factors, 4 (2²) and 6 (2×3) give an LCD of 12․ Understanding this step is essential for mastering fraction operations․
2․3․ Rewriting Fractions with the Common Denominator
Once the Least Common Denominator (LCD) is identified, the next step is to rewrite each fraction with this common denominator․ This ensures that the fractions have the same base, making addition or subtraction straightforward․ To rewrite a fraction, divide the LCD by the original denominator to find the multiplier․ Multiply both the numerator and the denominator of the fraction by this number to create an equivalent fraction․ For example, to rewrite 1/4 and 1/6 with an LCD of 12, multiply 1/4 by 3/3 and 1/6 by 2/2, resulting in 3/12 and 2/12․ This step is essential for aligning the fractions and simplifying the calculation․

Steps to Add and Subtract Fractions with Unlike Denominators

Adding and subtracting fractions with different denominators involves finding a common denominator, rewriting each fraction, and then performing the arithmetic on the numerators before simplifying the result․
3․1․ Step 1: Identify the Denominators
Begin by identifying the denominators of the fractions involved in the problem․ This step is crucial as it sets the foundation for finding a common denominator․ For example, if you’re adding ( rac{1}{4} ) and ( rac{3}{6} ), the denominators are 4 and 6․ Understanding the denominators helps determine the next steps in the process․ Always ensure the denominators are clear before proceeding to avoid errors in calculations․ This initial identification simplifies the subsequent steps of finding the least common multiple and rewriting the fractions․ Clear denominators lead to accurate and efficient problem-solving in fraction operations․
3․2․ Step 2: Find the Least Common Multiple (LCM)
After identifying the denominators, the next step is to find their Least Common Multiple (LCM)․ The LCM is the smallest number that both denominators can divide into without leaving a remainder․ For example, if the denominators are 4 and 6, the multiples of 4 are 4, 8, 12, 16, and the multiples of 6 are 6, 12, 18․ The smallest common multiple is 12, so the LCM is 12․ Finding the LCM ensures that the fractions can be rewritten with the same denominator, making addition or subtraction straightforward․ This step is essential for simplifying the fractions and performing accurate calculations․
3․3․ Step 3: Convert Fractions to Equivalent Fractions
Once the LCM is determined, the next step is to convert each fraction into an equivalent fraction with the common denominator․ To do this, multiply both the numerator and the denominator of each fraction by the same number to reach the LCM․ For example, if the fractions are 1/4 and 1/6, and the LCM is 12, multiply the first fraction by 3/3 to get 3/12 and the second fraction by 2/2 to get 2/12․ This ensures both fractions have the same denominator, making them equivalent fractions․ The value of the fractions remains the same, but now they can be easily added or subtracted․ This step is crucial for accurate calculations in fraction operations․
3․4․ Step 4: Perform the Addition or Subtraction
After converting fractions to equivalent forms with a common denominator, the final step is to perform the addition or subtraction․ For addition, add the numerators while keeping the denominator the same․ For subtraction, subtract the numerators while maintaining the denominator․ For example, if adding 3/12 and 2/12, the result is 5/12․ If subtracting, 5/12 minus 2/12 equals 3/12․ Simplify the resulting fraction if possible․ This step requires attention to detail to ensure accuracy, especially with mixed numbers or larger numerators․ Practice with worksheets helps build confidence in performing these operations correctly and efficiently; This step solidifies the understanding of fraction operations․
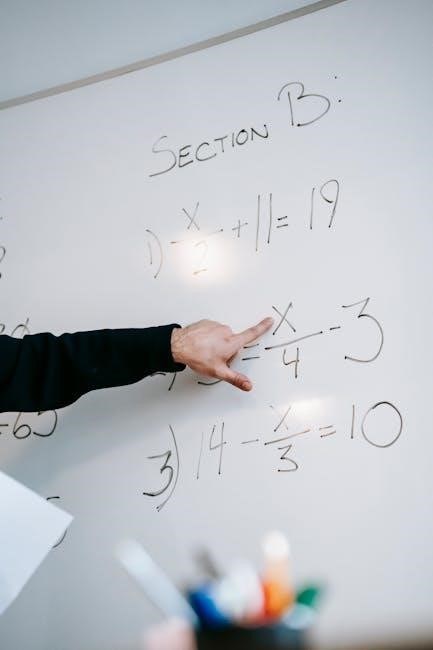
Worksheets for Practicing Fraction Operations
Discover a variety of worksheets designed to help students master adding and subtracting fractions with unlike denominators․ Suitable for different grade levels, these PDF resources include mixed numbers and multiple fractions, offering comprehensive practice for all skill levels․
4․1․ Basic Worksheets for Adding and Subtracting Fractions
Our basic worksheets are perfect for introducing students to adding and subtracting fractions with unlike denominators․ These PDF resources feature clear instructions and step-by-step examples, ensuring a solid foundation in fraction operations․ With a focus on simplicity, they cover essential concepts like finding the least common denominator and converting fractions․ Ideal for younger learners or those needing a refresher, these worksheets are designed to build confidence and fluency in handling fractions with different denominators․ Each exercise is carefully crafted to reinforce key skills, making them an excellent starting point for fraction mastery;

4․2․ Worksheets with Mixed Numbers and Unlike Denominators
These worksheets challenge students to add and subtract mixed numbers and fractions with unlike denominators․ They offer a mix of straightforward and complex problems, ensuring a comprehensive understanding of fraction operations․ By practicing with mixed numbers, students learn to handle both whole numbers and fractional parts seamlessly․ The exercises are designed to enhance problem-solving skills and apply fraction concepts to real-world scenarios․ Each worksheet provides ample opportunities to convert mixed numbers to improper fractions and vice versa, solidifying this critical skill for advanced fraction operations․
4․3․ Advanced Worksheets for Combining Multiple Fractions

For students ready to tackle more complex challenges, these advanced worksheets focus on adding and subtracting multiple fractions with unlike denominators․ They include scenarios with three or more fractions, requiring the identification of the least common denominator and precise calculation․ These exercises are ideal for reinforcing skills in handling multi-step fraction operations and preparing for higher-level math․ The problems are varied, ensuring a deep understanding of fraction manipulation and application in real-world contexts, such as measurements and financial calculations․ Each worksheet builds confidence in tackling intricate fraction problems with accuracy and speed․
Benefits of Using Worksheets for Learning Fraction Operations
Worksheets enhance understanding of fraction concepts, improve problem-solving skills, and promote retention of mathematical processes through structured and repetitive practice, making learning engaging and effective․
5․1․ Improved Understanding of Fraction Concepts
Worksheets designed for adding and subtracting fractions with unlike denominators help students grasp fundamental fraction concepts․ By practicing with structured problems, learners develop a clear understanding of equivalent fractions, the importance of common denominators, and how to manipulate numerators while keeping the denominator consistent․ Visual aids and step-by-step exercises in worksheets make abstract fraction operations more tangible, enabling students to recognize patterns and relationships between different fractions․ This focused practice builds confidence and clarifies misconceptions, ensuring a strong foundation for more complex mathematical tasks․ Over time, consistent use of worksheets fosters a deeper appreciation for how fractions apply to real-world scenarios, making learning both meaningful and engaging․
5․2․ Enhanced Problem-Solving Skills
Engaging with worksheets focused on adding and subtracting fractions with unlike denominators enhances problem-solving abilities․ These exercises require students to apply critical thinking and logical reasoning to find common denominators, convert fractions, and perform calculations․ By breaking down problems into manageable steps, learners develop a systematic approach to tackling complex fraction operations․ Worksheets also encourage the use of visual aids and number sense to verify results, fostering accuracy and mathematical intuition․ Regular practice builds confidence and fluency, enabling students to apply these skills to real-world scenarios and more advanced mathematical challenges with ease․ This structured practice helps refine problem-solving techniques, ensuring long-term mastery of fraction operations․
5․3․ Better Retention of Mathematical Processes
Using worksheets to practice adding and subtracting fractions with unlike denominators significantly improves the retention of mathematical processes․ Regular practice reinforces the steps involved in finding common denominators, converting fractions, and performing operations․ Repetition strengthens memory and ensures that these processes become second nature․ Worksheets also provide a structured format, helping students organize their thoughts and approach problems methodically․ Over time, this consistent practice leads to long-term retention of fraction operations, making it easier to apply these skills in more complex mathematical scenarios․ The clarity and repetition offered by worksheets are key to mastering and retaining these essential fraction skills․ This structured learning fosters confidence and proficiency in mathematical problem-solving․

Real-World Applications of Fraction Operations
Fractions are essential in everyday tasks like cooking, construction, and budgeting․ Mastering adding and subtracting fractions with unlike denominators helps solve real-world problems efficiently and accurately; Practical applications make learning fractions meaningful and relevant․
6․1․ Everyday Uses of Fractions
Fractions play a crucial role in daily life, making tasks more manageable․ In cooking, adjusting recipes requires adding or subtracting fractions, like doubling ingredients․ Construction workers use fractions to measure materials accurately․ Budgeting and shopping involve comparing prices and quantities, often relying on fraction operations․ Word problems in real-life scenarios, such as dividing resources or calculating distances, frequently involve unlike fractions․ Mastery of these skills enhances problem-solving abilities, making everyday tasks easier and more efficient․ By practicing with worksheets, students develop the skills needed for practical applications, ensuring they can handle real-world challenges confidently․ Fractions are not just academic concepts but essential tools for navigating life’s demands․
6․2․ Word Problems Involving Unlike Fractions
Word problems involving unlike fractions require practical application of fraction operations․ These problems often appear in real-world scenarios, such as dividing resources, budgeting, or adjusting recipes․ For example, if a recipe calls for 1/4 cup of sugar and another requires 3/8 cup, adding these fractions is essential for scaling the recipe correctly․ Similarly, construction projects may involve calculating materials using unlike fractions․ Worksheets provide structured practice for solving such problems, ensuring students can apply fraction concepts effectively․ By mastering these skills, learners develop the ability to tackle complex, real-world challenges confidently, making fractions a vital tool in everyday problem-solving and decision-making processes․
Practice is essential for mastering fraction operations, especially when dealing with unlike denominators․ Consistent practice builds confidence and fluency in handling complex fraction problems․ Worksheets provide structured exercises that help reinforce fraction concepts, enabling students to apply them to real-world scenarios․ Regular practice improves problem-solving skills and enhances retention of mathematical processes․ While mastering fractions may seem challenging, dedicated practice ensures long-term understanding and proficiency․ By engaging with worksheets and exercises, students can overcome difficulties and develop a strong foundation in fraction operations, ultimately becoming adept at solving even the most intricate mathematical tasks with ease and accuracy․
