Soliton gas, crucial for the Nonlinear Schrödinger Equation (NLSE), describes numerous interacting solitons; its PDF reveals statistical properties vital for understanding wave phenomena.
The Journal of Nonlinear Waves publishes authoritative articles on theoretical and computational aspects of nonlinear waves, including soliton gas research.
Understanding the soliton structure is fundamental, as its shape remains unchanged after collisions, a key feature in integrable systems and PDF analysis.
Background of the Nonlinear Schrödinger Equation (NLSE)
The NLSE, a cornerstone in soliton gas studies, initially emerged in the realm of water wave mechanics, describing the propagation of nonlinear waves. Its adaptability extends to diverse fields like optical fiber communication and Bose-Einstein condensates.
Crucially, the NLSE’s integrability allows for exact solutions, including solitons, enabling the investigation of their interactions and statistical behavior, vital for constructing a PDF.
The equation’s significance lies in modeling systems where dispersion and nonlinearity balance, leading to stable wave structures – the foundation of soliton gas dynamics and its probabilistic description.
The Concept of Solitons
Solitons are localized, stable waves maintaining their shape and speed during propagation, even after collisions – a remarkable characteristic differentiating them from typical waves. This stability arises from a delicate balance between dispersive and nonlinear effects.
In the context of the NLSE, solitons represent fundamental building blocks for constructing a soliton gas. Their interactions, described statistically, are key to understanding the overall wave dynamics and forming the PDF.
Understanding soliton behavior is crucial, as they represent coherent structures within the broader, seemingly random, distribution of a soliton gas.
What is a Soliton Gas?
A soliton gas emerges when a large number of solitons coexist and interact within a nonlinear system governed by the NLSE. Unlike isolated solitons, a gas exhibits collective behavior, resembling a statistical ensemble.
The statistical properties, particularly the Probability Density Function (PDF), are vital for characterizing the distribution of soliton characteristics like amplitude and density. Analyzing this PDF reveals insights into wave turbulence.
Essentially, it’s a weakly turbulent state where soliton interactions are frequent but do not lead to complete wave destruction.

Mathematical Framework of Soliton Gas
NLSE derivation utilizes the Inverse Scattering Transform (IST) and Lax Pair, enabling analysis of soliton interactions and the PDF of soliton gas solutions.
Derivation of the NLSE
The Nonlinear Schrödinger Equation (NLSE) emerges from considering wave propagation in nonlinear media, balancing dispersion and nonlinearity. Starting with the classical wave equation, incorporating a Kerr nonlinearity term – representing intensity-dependent refractive index – yields the fundamental NLSE form.
Further mathematical manipulation, often involving Fourier transforms and careful consideration of the physical parameters, leads to the canonical NLSE. This equation is pivotal for modeling soliton gas dynamics, as it governs the evolution of wave packets and their interactions, ultimately influencing the probability density function (PDF).
Understanding this derivation is crucial for interpreting the PDF and its relation to the underlying physics.
The Inverse Scattering Transform (IST)
The Inverse Scattering Transform (IST) provides a powerful method for solving the Nonlinear Schrödinger Equation (NLSE), crucial for analyzing soliton gas behavior. It involves solving a linear scattering problem associated with the NLSE and then reconstructing the solution from the scattering data.
IST elegantly reveals the soliton solutions and their interactions, offering insights into the long-time dynamics. This method is fundamental for calculating the probability density function (PDF) of the soliton gas, as it allows for precise determination of soliton positions and velocities.
The IST is key to understanding the statistical properties.
The Role of the Lax Pair
The Lax Pair, a cornerstone of integrability, plays a vital role in understanding the soliton gas solutions of the Nonlinear Schrödinger Equation (NLSE). It consists of a pair of operators whose commutation relation guarantees the existence of conserved quantities, ensuring soliton stability.
This framework is essential for deriving the Inverse Scattering Transform (IST) and, consequently, for calculating the probability density function (PDF) describing the soliton gas. The Lax Pair’s structure dictates the soliton interactions and their phase shifts.
It’s fundamental for statistical analysis.

Properties of Soliton Gas Solutions
Soliton gas solutions exhibit unique interactions and phase shifts, crucial for understanding their statistical properties and the resulting probability density function (PDF).
Analyzing soliton density and distribution is key to characterizing the PDF shape.
Soliton Interactions and Phase Shifts
Soliton interactions within a soliton gas are remarkably elastic; they maintain shape post-collision, differing only in phase. These phase shifts are pivotal for determining the statistical properties and ultimately, the probability density function (PDF).
The NLSE governs these interactions, and understanding them is crucial for accurately modeling the soliton gas. Analyzing these shifts allows for a deeper comprehension of the underlying wave dynamics and the resulting PDF characteristics, essential for applications.
These interactions are fundamental to the soliton gas behavior.
Statistical Properties of Soliton Gas
The statistical properties of a soliton gas, governed by the Nonlinear Schrödinger Equation (NLSE), are primarily characterized by its probability density function (PDF). This PDF describes the distribution of soliton parameters, like amplitude and velocity, revealing crucial insights into the gas’s overall behavior.
Analyzing these properties is vital for understanding phenomena like rogue wave formation. The Journal of Nonlinear Waves publishes research detailing these statistical analyses, offering a deeper understanding of the soliton gas.
These properties define the gas’s dynamics.
Density and Distribution of Solitons
Determining the density and distribution of solitons within a soliton gas, described by the Nonlinear Schrödinger Equation (NLSE), is central to understanding its behavior. The probability density function (PDF) plays a key role, revealing how solitons are spatially arranged and their concentration levels.
Research published in the Journal of Nonlinear Waves explores these distributions, offering insights into the gas’s statistical mechanics. Understanding these aspects is crucial for predicting wave dynamics and rogue wave occurrences.
Soliton density impacts overall gas properties.

Applications of Soliton Gas in Physics
Soliton gas, modeled by the NLSE, finds applications in optical fiber communication, Bose-Einstein condensates, and water wave dynamics, informing PDF-based predictions.
Optical Fiber Communication
Soliton gas solutions, derived from the Nonlinear Schrödinger Equation (NLSE), are profoundly relevant to optical fiber communication systems. These systems leverage the stability of solitons to transmit information over long distances with minimal signal degradation.
The PDF characterizing the soliton gas helps predict the statistical distribution of pulse intensities, crucial for optimizing transmission parameters and mitigating the effects of noise and nonlinearities. Understanding soliton interactions, modeled through the NLSE, is vital for designing robust and efficient fiber optic networks.
Furthermore, analyzing the soliton gas’s properties aids in predicting and managing the emergence of rogue waves, which can disrupt data transmission.
Bose-Einstein Condensates
Bose-Einstein Condensates (BECs) provide a fascinating physical system where the Nonlinear Schrödinger Equation (NLSE) and soliton gas dynamics find compelling applications. The collective behavior of bosons can be effectively modeled using the NLSE, revealing the emergence of soliton-like excitations.
The PDF describing the soliton gas in BECs offers insights into the statistical properties of these excitations, influencing the condensate’s stability and response to perturbations. Analyzing these distributions helps understand the complex interactions within the condensate.
These insights are crucial for controlling and manipulating BECs for quantum computing and sensing applications.
Water Wave Dynamics and Rogue Waves
Soliton gas concepts, derived from the Nonlinear Schrödinger Equation (NLSE), offer a framework for understanding complex water wave dynamics, particularly the emergence of rogue waves. These unexpectedly large waves, appearing suddenly, can be statistically described using the soliton gas PDF.
The PDF reveals the probability of extreme wave events, providing valuable insights into their occurrence and potential hazards. Analyzing the soliton gas as a precursor to rogue waves helps predict their formation.
The Peregrine soliton, a specific solution, exemplifies this connection.
Numerical Methods for Studying Soliton Gas
Direct Numerical Simulation, Split-Step Fourier, and Monte Carlo methods are vital for analyzing soliton gas solutions derived from the NLSE and its PDF.
Direct Numerical Simulation
Direct Numerical Simulation (DNS) offers a foundational approach to studying soliton gas dynamics, directly solving the Nonlinear Schrödinger Equation (NLSE) without modeling turbulence.
This method, while computationally intensive, provides detailed insights into soliton interactions and the evolution of the Probability Density Function (PDF). DNS accurately captures complex phenomena, enabling validation of simplified models.
However, its high computational cost limits its application to relatively small systems and short timescales, hindering long-term statistical analysis of the soliton gas.
Split-Step Fourier Method
The Split-Step Fourier Method (SSFM) is a widely used numerical technique for solving the Nonlinear Schrödinger Equation (NLSE), offering a balance between accuracy and computational efficiency when studying soliton gas.
SSFM alternates between linear and nonlinear propagation steps, leveraging the Fourier transform to efficiently handle the linear part and directly integrating the nonlinear term.
This allows for simulations over longer distances and timescales than Direct Numerical Simulation, facilitating the study of PDF evolution and statistical properties of the soliton gas.
Monte Carlo Simulations
Monte Carlo Simulations provide a statistical approach to studying soliton gas behavior, particularly useful for analyzing the Probability Density Function (PDF) and related statistical properties of the Nonlinear Schrödinger Equation (NLSE).
These simulations involve generating numerous random initial conditions and evolving them using numerical methods like the Split-Step Fourier Method, then statistically analyzing the resulting soliton distributions.
This method is valuable for validating analytical approximations of the PDF and exploring parameter regimes inaccessible to other techniques, offering insights into rogue wave precursors.
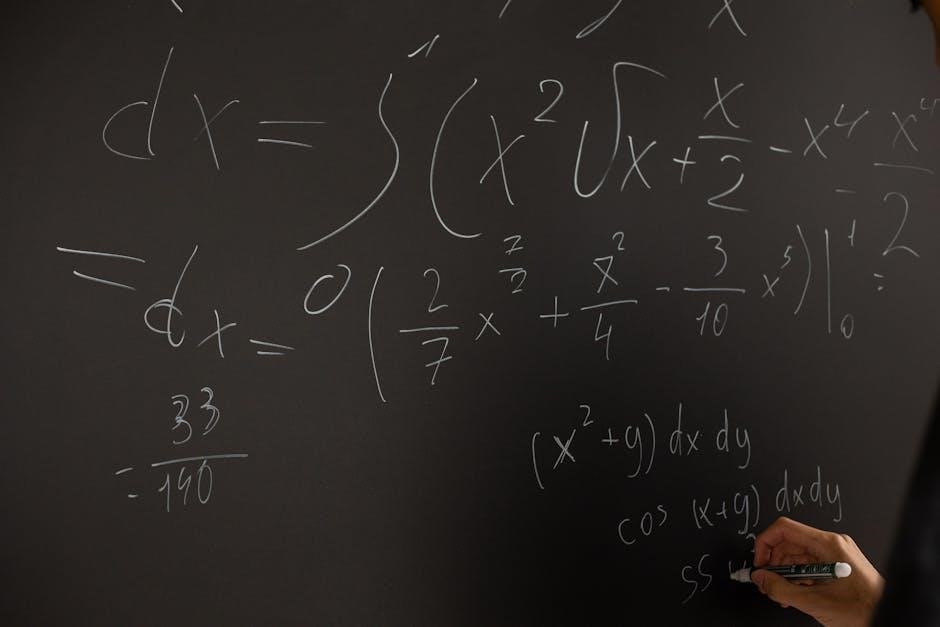
The PDF of Soliton Gas Solutions
Understanding the Probability Density Function (PDF) is vital for characterizing soliton gas, revealing statistical properties of NLSE solutions and soliton distributions.
Analytical approximations and Monte Carlo Simulations help define the PDF shape, impacted by system parameters.
Understanding the Probability Density Function
The Probability Density Function (PDF) is central to characterizing soliton gas solutions for the Nonlinear Schrödinger Equation (NLSE). It provides a statistical description of soliton distribution, revealing insights into wave phenomena and their long-term behavior.
Analyzing the PDF allows researchers to quantify the likelihood of observing specific soliton densities and configurations. This is crucial for understanding the emergence of extreme events, like rogue waves, which are statistically rare but impactful.
Determining the PDF often involves complex mathematical techniques and numerical simulations, aiming to capture the intricate interplay between solitons within the gas.
Analytical Approximations of the PDF
Analytical approximations of the Probability Density Function (PDF) for soliton gas solutions are vital, offering simplified representations of complex statistical distributions derived from the Nonlinear Schrödinger Equation (NLSE).
These approximations, often based on asymptotic analysis or statistical mechanics, provide valuable insights without the computational cost of full numerical simulations. Common approaches include utilizing Gaussian or exponential functions to model the PDF’s shape.
However, accuracy depends on parameter regimes and assumptions, necessitating careful validation against numerical results and experimental observations.
Impact of Parameters on the PDF Shape
Parameters significantly influence the Probability Density Function (PDF) shape of soliton gas solutions derived from the Nonlinear Schrödinger Equation (NLSE). Key factors include spectral density, nonlinearity strength, and dissipation levels.
Increased nonlinearity generally leads to broader PDFs with heavier tails, indicating a higher probability of extreme events like rogue waves. Varying spectral density alters the soliton density and distribution, impacting the PDF’s overall form.
Dissipation introduces damping, affecting soliton lifetimes and consequently, the PDF characteristics.
Recent Research and Developments
Recent studies, published in the Journal of Nonlinear Waves, focus on refining PDF approximations for soliton gas, enhancing understanding of extreme wave statistics.
Emerging trends involve advanced numerical methods for accurate PDF calculations.
Journal of Nonlinear Waves and Related Publications
The Journal of Nonlinear Waves serves as a premier venue for disseminating cutting-edge research on soliton gas solutions to the Nonlinear Schrödinger Equation (NLSE). It publishes authoritative articles detailing both theoretical advancements and computational explorations of these complex wave phenomena.
Recent issues feature studies focused on characterizing the Probability Density Function (PDF) of soliton distributions, crucial for understanding rogue wave statistics. Related publications appear in journals like Physical Review Letters and Chaos, often referencing work initially presented within the Journal of Nonlinear Waves.
Emerging Trends in Soliton Gas Research
Current research increasingly focuses on refining analytical approximations of the Probability Density Function (PDF) describing soliton gas solutions to the Nonlinear Schrödinger Equation (NLSE). Investigations explore the PDF’s sensitivity to varying system parameters, impacting soliton interactions.
A significant trend involves developing more efficient numerical methods for simulating soliton gas dynamics, alongside studies linking soliton gas behavior to the emergence of rogue waves. The Journal of Nonlinear Waves actively showcases these advancements.
Open Problems and Future Directions
Key challenges remain in accurately predicting the Probability Density Function (PDF) of soliton gas solutions for the Nonlinear Schrödinger Equation (NLSE), particularly in complex, multi-dimensional systems. Further research is needed to address the computational complexity of simulations.
Future work should explore the impact of dissipation and gain on soliton gas statistics and refine models for rogue wave prediction, leveraging publications in the Journal of Nonlinear Waves to guide progress.

Connection to Rogue Wave Phenomena
Soliton gas can precede rogue waves; statistical descriptions detail their occurrence, with the Peregrine soliton as a fundamental example, impacting PDF analysis.
Soliton Gas as a Precursor to Rogue Waves
Soliton gas dynamics offer insights into the emergence of rogue waves, extraordinarily high and steep isolated waves appearing suddenly. The statistical properties derived from the PDF of the soliton gas reveal conditions conducive to rogue wave formation.
Specifically, fluctuations within the soliton gas, characterized by varying soliton densities and interactions, can constructively interfere, amplifying wave amplitudes. This process, modeled through the Nonlinear Schrödinger Equation, demonstrates how a seemingly random distribution of solitons can coalesce into a localized, intense rogue wave.
Understanding this connection is crucial for predicting and potentially mitigating the risks associated with these unpredictable oceanic events.
Statistical Description of Rogue Wave Occurrence
The probability density function (PDF) of a soliton gas provides a statistical framework for describing rogue wave occurrences. Analyzing the PDF’s tails reveals the likelihood of extreme events, like exceptionally high waves, exceeding predefined thresholds.
This statistical approach, rooted in the Nonlinear Schrödinger Equation, moves beyond deterministic predictions, acknowledging the inherent randomness in wave dynamics. The PDF allows for estimating return periods – the average time between rogue wave events – crucial for risk assessment.
Furthermore, parameters influencing the PDF shape dictate rogue wave frequency and intensity.
The Peregrine Soliton
The Peregrine soliton, a fundamental solution to the Nonlinear Schrödinger Equation (NLSE), represents the highest theoretically possible single wave. Its emergence within a soliton gas is statistically linked to the probability density function (PDF), specifically its extreme value statistics.
The PDF predicts the probability of finding such a localized, high-amplitude wave. Understanding the conditions leading to Peregrine soliton formation is vital for modeling rogue wave phenomena.
Its unique shape and dynamics offer insights into energy focusing mechanisms within the soliton gas.

Computational Tools and Software
MATLAB and Python libraries facilitate NLSE solving, aiding soliton gas studies and PDF analysis; specialized software enhances simulations.
TradingView provides real-time data for financial analysis, including stock information like Macquarie Infrastructure (088980).
MATLAB Implementations
MATLAB offers robust tools for simulating soliton gas dynamics governed by the Nonlinear Schrödinger Equation (NLSE). Researchers utilize custom scripts and toolboxes to implement the Inverse Scattering Transform (IST), crucial for obtaining soliton solutions and analyzing their interactions.
These implementations allow for the computation of the Probability Density Function (PDF) of soliton distributions, revealing statistical properties like density and soliton interactions. Visualizations aid in understanding the complex behavior of the soliton gas, furthering research into wave phenomena.
Furthermore, MATLAB’s capabilities support the exploration of parameters influencing the PDF shape, providing insights into the system’s characteristics.
Python Libraries for NLSE Solvers
Python provides several libraries ideal for simulating soliton gas behavior within the Nonlinear Schrödinger Equation (NLSE) framework. Packages like NumPy and SciPy offer fundamental numerical computation tools, while specialized libraries facilitate IST implementation and soliton tracking.
These tools enable researchers to compute the Probability Density Function (PDF), characterizing soliton distributions and interactions. Visualization libraries, such as Matplotlib, aid in analyzing the soliton gas and understanding the PDF’s shape.
Efficiently exploring parameter spaces impacting the PDF becomes readily achievable with Python’s versatility.
Specialized Software Packages
Beyond Python and MATLAB, specialized software packages cater to advanced soliton gas and NLSE simulations. These often incorporate optimized algorithms for the Inverse Scattering Transform (IST), crucial for analyzing soliton interactions and generating accurate Probability Density Functions (PDFs).
Such packages frequently offer pre-built functionalities for calculating statistical properties, visualizing soliton distributions, and exploring the impact of various parameters on the PDF shape.
They streamline complex computations, accelerating research into soliton gas dynamics.

Challenges and Limitations
Computational complexity hinders large-scale soliton gas simulations, impacting PDF accuracy. Stability issues in numerical methods and model physical realism pose further constraints.
Computational Complexity
Simulating soliton gas demands significant computational resources due to the numerous interacting solitons and long timescales required to achieve statistically meaningful results for the PDF. The Inverse Scattering Transform (IST), while theoretically elegant, becomes computationally expensive for large systems.
Direct numerical simulations of the Nonlinear Schrödinger Equation (NLSE) necessitate fine spatial and temporal discretization, escalating computational costs. Accurately resolving soliton interactions and capturing the evolving PDF requires substantial memory and processing power, limiting the size and duration of simulations.
Efficient algorithms and parallel computing are crucial for tackling this complexity, but remain a significant hurdle in studying soliton gas behavior.
Accuracy and Stability of Numerical Methods
Numerical simulations of soliton gas, aiming to accurately represent the PDF, face challenges regarding accuracy and stability. The Split-Step Fourier Method, commonly used for the NLSE, can introduce errors due to discretization and nonlinear term handling.
Maintaining stability over long simulation times is critical for capturing the statistical properties of the soliton gas. Small numerical errors can grow, distorting the PDF and leading to inaccurate predictions.
Careful selection of numerical parameters and robust algorithms are essential for reliable results.
Physical Realism of the Model
The NLSE, foundational for soliton gas studies and PDF analysis, is an idealized model. Real-world systems often include dissipation, gain, and higher-order effects absent in the basic equation. These factors influence soliton interactions and the overall statistical distribution.
While the soliton gas provides valuable insights, its physical realism is limited. Accurately representing phenomena like rogue wave precursors requires incorporating more complex physical mechanisms.
Bridging the gap between theoretical models and experimental observations remains a significant challenge.

Advanced Topics in Soliton Gas Theory
Higher-order NLSE extensions and multi-dimensional systems refine soliton gas modeling. Investigating dissipation/gain effects impacts PDF characteristics and wave dynamics.
Higher-Order NLSE
Higher-order Nonlinear Schrödinger Equations (NLSE) introduce terms beyond the quadratic nonlinearity, impacting soliton gas dynamics. These extensions account for effects like third-order dispersion and self-steepening, altering soliton interactions and stability.
Consequently, the Probability Density Function (PDF) of soliton distributions shifts, deviating from predictions based on the standard NLSE. Analyzing these higher-order effects is crucial for accurately modeling complex wave phenomena and refining soliton gas theory.
Such refinements are essential for applications in optical fiber communication and understanding rogue wave formation.
Soliton Gas in Multi-Dimensional Systems
Extending soliton gas concepts to two or three dimensions significantly complicates the analysis, introducing new interaction dynamics and spatial effects. The Probability Density Function (PDF) becomes more complex, reflecting the increased degrees of freedom and potential for collisions.
Multi-dimensional systems exhibit phenomena absent in one dimension, like soliton vortex formation and transverse instabilities, influencing the soliton gas’s statistical properties. Accurate modeling requires advanced numerical techniques and careful consideration of boundary conditions.
These systems are relevant to diverse physical scenarios.
The Effect of Dissipation and Gain
Introducing dissipation and gain into the Nonlinear Schrödinger Equation (NLSE) fundamentally alters soliton gas dynamics, moving away from the purely integrable regime. Dissipation leads to soliton decay and energy loss, impacting the Probability Density Function (PDF) by reducing soliton density.
Conversely, gain can stabilize solitons and even induce soliton proliferation, shifting the PDF towards higher amplitudes. The interplay between dissipation and gain creates a non-equilibrium soliton gas, requiring specialized analytical and numerical approaches.
These effects are crucial in realistic systems.

Resources for Further Study
Key textbooks on nonlinear optics and online courses provide essential foundations. The Journal of Nonlinear Waves offers cutting-edge research on soliton gas and the NLSE.
Key Textbooks on Nonlinear Optics
Several textbooks are invaluable for understanding soliton gas and the Nonlinear Schrödinger Equation (NLSE). “Optical Solitons” by Govind Agrawal provides a comprehensive treatment of soliton dynamics in optical fibers, crucial for grasping the underlying physics.
Additionally, “Nonlinear Fiber Optics” by John H. Marburger explores advanced topics, including the Inverse Scattering Transform (IST), essential for analyzing soliton gas solutions. These resources, alongside articles in the Journal of Nonlinear Waves, offer a strong foundation for research.
Online Courses and Tutorials
Numerous online resources supplement textbook learning for soliton gas and the NLSE. Platforms like Coursera and edX offer courses on nonlinear optics and wave phenomena, covering foundational concepts.
MIT OpenCourseWare provides lecture notes and materials on related topics, including the Inverse Scattering Transform. Furthermore, specialized tutorials focusing on numerical methods, like the Split-Step Fourier Method, are available, aiding in PDF analysis and simulations.
